Fluid Types and Properties [Complete Explained]
What is fluid?
Fluid Types and Properties :- Any substance which can flow or undergoing relative change of position of particle with respect to time is known as fluid. Fluid can be liquid or gas because both of them posses the property to flow continuously. Fluid does not have any certain shape, it occupies the shape of container and it can flows under its own weight.
In fluid mechanics, we study the effect of force on fluid and it can be further divided into two types. When fluid is at rest then the study is known as fluid statics, when fluid is in motion then the study is known as fluid dynamics.
There are mainly two types of approaches of the study of fluid. They are –
- Microscopic approach: In microscopic approach the study of fluid is done at the microscopic level. Analysis is done separately of the individual particles then their average is taken and based on their molecular behavior, their different properties are determined.
- Macroscopic approach: In Macroscopic approach study is not done on microscopic level. In Macroscopic approach we study average behavior of fluid or the overall behavior of fluid.
In this approach, we assume that that the fluid contain very large size molecules, larger than the voids present. So, we assume that there are no voids and the molecules are continuous which is called continuous distribution of mass. For the determination of where we can apply this macroscopic approach, we have a dimensionless parameter known as Knudsen number (it is represented by ku)
Knudsen number is the ratio of mean free path to characteristic length. Mean free path is the distance travelled by the molecule during two consecutive collisions. Characteristic length is the length in which our concerned fluid is being analyzed.
Example 1. (Fluid Types and Properties)
If the value of ku is less than 0.01 then the voids between the fluids is negligible and we can call it continuous distribution of mass or continuum. In this case the first particle flowing over the solid surface is assumed to adhere and velocity of that layer is reduced to zero.
Continuum is beneficial for us because if there is gap between the molecules then properties of fluids like density, specific gravity, mass, specific volume are discontinuous.
For mathematical approaches like integration and differentiation applied on fluid we need the function to be a continuous function. If there is gap or they are discontinuous then application of mathematical approaches like integration and differentiation are difficult.
Example 2. (Fluid Types and Properties)
When ku is more than 0.01 and less than 10 then the fluid flow is called slip flow. In this case the adjacent fluid layer of the solid surface is assumed to be not adhering to the solid surface and velocity of the layer is not reduced to zero completely, they slip over the solid surface that’s why they are called slip flow.
Example 3. (Fluid Types and Properties)
If ku is greater than 10 then the flow is called free molecular flow, more the value of ku means more is the length of mean free path .This means that the speed of molecules is very large so it is very difficult to analyze them and in this case macroscopic approach is not useful.
There are two types of forces acting on the body of fluid
i) Surface force: It acts on the surface of fluid (Atmospheric force).
ii) Body force: It acts on the mass of the fluid (Gravitational force).
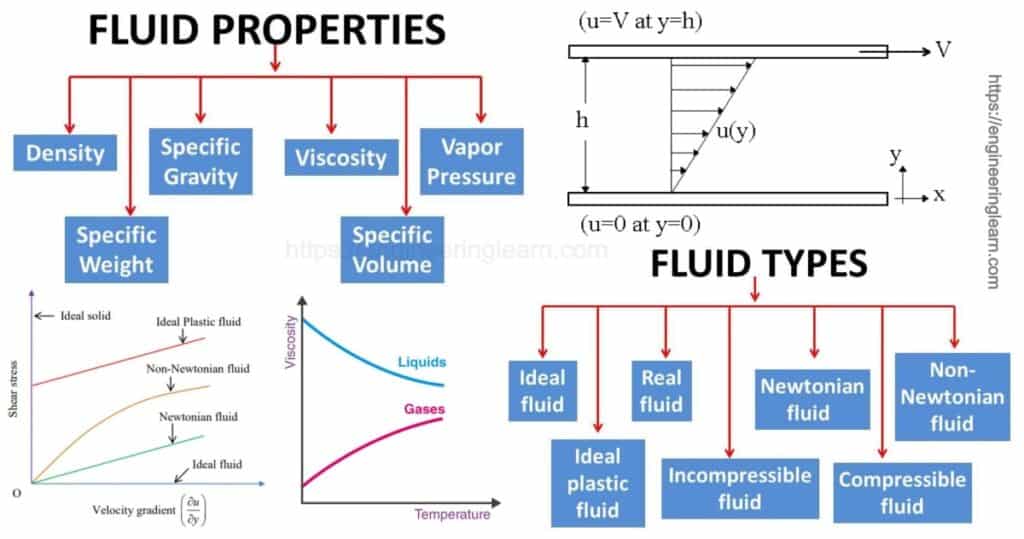
Properties of Fluid
1. Density or Mass Density (ρ)
Density is defined as the ratio of mass per unit volume. It states the compactness of substance or mass present in the given volume.
Density= Mass/ Volume
SI unit of density is kg/m³
NOTE: Density of water is 1000 kg/m³ at 4ºC and 997 kg/m³ at 25ºC
2. Weight Density (γ)
Weight density is defined as the ratio of weight per unit volume
Weight density= Weight/ Volume
SI unit of weight density is N/m³
γ = W/V = mg/V = ρg
Therefore γ= ρg
3. Specific Gravity
Specific gravity is defined as the ratio of the density of a fluid to the density of standard fluid at standard temperature pressure (STP)
Specific gravity= Density of fluid/ Density of standard fluid
a) For liquid
Specific gravity of liquid= density of liquid/ density of water at 4ºC
b) For gas
Specific gravity of gas= density of gas/ density of air at STP
Density of water at STP is 1000 kg/m³
Density of air at STP is 1.21 kg/m³
4. Surface Tension (σ)
Free surface of a liquid behaves like a stretched membrane and it tries to minimize its area, up to maximum possible extent, this property is known as surface tension.
Mathematically,
Surface tension= Force/ Length
SI unit is N/m
Free surface is the surface with constant normal stress (due to atmospheric pressure) and zero shear stress (because no external force in tangential direction).
Two points A and B are taken for consideration. At point B, the molecule at B experiencing molecular attraction force (due to cohesion) exerted by the neighboring molecule in every possible direction. Therefore summation of forces at point B is zero which means molecule at point B is in equilibrium and not moving because net force is zero.
But when we consider the molecule at point A which is at free surface the pull forces exerted by the neighboring molecule is not symmetrical, therefore summation of force at point A is not equal to zero and we have a resultant force acting downward.
So we have same behavior of molecules present at free surface having downward resultant force and this force try to contract the surface and this property is called surface tension.
Surface Tension in Different Cases
a) Water Droplet: (Fluid Types and Properties)
As we know surface tension is a inward pull acting at free surface.
For equilibrium condition, outward pressure (Po) on water droplet should be equal to inward pressure (Pi) because if there is some net force then water droplet collapse.
Pi= Po
ΣF=0
Therefore, Pressure force= Force due to surface tension
P x πR²= σ x 2πR (Number of free surface in case of water droplet is one)
P = 2σ/R
b) Soap Bubble: (Fluid Types and Properties)
In case of soap bubble, air is present inside the bubble as well as outside the bubble. So the inside surface of the bubble is also a free surface. Therefore we have two free surfaces.
Surface tension occurs only in liquid and in case of gases value of surface tension is negligible or zero because the position of molecule in gases changes time to time and distance is not confined while in case of liquid distance between the molecules is confined.
Thickness of soap bubble is negligible therefore the radius of outer surface and inner surface is same.
For equilibrium,
P x πR²= σ x (2 x 2πR)
P = 4σ/R
c) Water Jet: (Fluid Types and Properties)
Jet shape is assumed to be cylindrical having inside pressure Pi and outside pressure Po. It has only one free surface because it is filled with liquid.
For equilibrium,
P x 2RL= σ x 2L
Where L= length of water jet
R= Radius of water jet
P = σ/R
5. Capillarity
Capillarity is defined as the phenomenon of rise or fall of liquid surface in a small tube relative to adjacent level of liquid when tube is held vertical.
- When adhesion force is significantly greater than cohesion force then liquid will wet the solid boundary, and the liquid is known as wetting liquid.
- When cohesion force is significantly greater than adhesion force then molecules of liquid exert cohesive force. This results in minimizing its area. This occurs specially in dense liquid like tar, grease etc., and the liquid is known as non wetting liquid.
r = Radius of capillary tube
R = Radius of curvature of meniscus
Capillary Rise/ Depression
d = Diameter of tube
ρ = Density of fluid
σ = Surface tension
NOTE: θ = 0º for water glass interface
θ = 128º For Mercury glass interface
6. Viscosity
It is defined as the resistance to flow of a fluid. There are two main reasons of viscosity
i) Cohesion: Attraction between particles of same matter (Prominent in liquids).
ii) Intermolecular momentum transfer: Gas molecule freely moves in a random path, according to the kinetic theory of gases. Hence the molecules of gases have kinetic energy when they are moving. Molecules of gases have particular mass and velocity therefore momentum of molecule is the product of mass and velocity.
When these gas molecules collide with each other they transfer momentum. The more they collide with each other, the more is the intermolecular friction between them. This results in viscosity in gases.
(Prominent in gases)
y = Distance perpendicular to solid boundary.
u = Velocity of fluid
Suppose a fluid is flowing in a solid surface. The very first layer of the fluid adheres with the solid surface and its velocity will be zero. Solid surface is exerting adhesive force, effect of adhesion forces disappear as we move above the solid surface and the velocity of the fluid increases. After observing velocity profile we have different value of velocity at different layer.
Arbitrarily taking two layers A and B. Layer A at the distance of y from solid surface and Layer B at the distance of y+dy from the solid surface. Thickness of layer dy.
Velocity of layer A is u and the velocity of layer B is u+du. From here we notice the velocity of layer A and layer B is different. So we conclude that layer B is moving with respect to layer A and there is a relative motion between layer A and layer B. As layer A is moving with lower velocity and layer B is moving with the higher velocity, B will experience a resistance in its motion. This resistance is known as viscosity.
Assuming a particle at initial position at 1 in the fluid element. When a very small force dF is applied. dτ shear stress produced due to the application of small force dF. We observe that fluid is not behaving like solid because in solid when we apply a force F then τ = F/A and the solid body gives a particular deformation (φ) and the value of φ depend upon a particular value of F. From Hooke’s law for solid shear stress is directly proportional to shear strain.
But in case of liquid strain is not constant for a particular value of F, value of strain is increasing with increase in time. Hence Hooke’s law is not applicable here. So we needed a law which explain this condition which is Newton’s Law of Viscosity.
NEWTON’S LAW OF VISCOSITY
Newton’s law of viscosity states that shear stress is directly proportional to the rate of shear strain.
Taking a small element of height dy and the velocity of a particular layer is du. Assuming a vertical line AB, our concerned particle is present at point B. velocity at point A is zero and velocity at point B is du. As we know fluid continuously deform under the action of a shear force. Velocity at point is B is du then at particular time interval dt it travels a distance of du x dt and occupy a new position which is point C.
ABC is a right angle triangle and θ is the shear strain at that particular instant.
Tan dθ = du.dt/ dy
As dθ is very small so tan dθ is equal to dθ
Therefore dθ = du.dt/ dy
dθ/dt = du/ dy
du = Change in velocity
dy = Distance
du/ dy = Change in velocity with respect to distance is known as velocity gradient.
dθ/ dt = Rate of shear strain
Therefore, from above equation we have
Rate of shear strain is equal to velocity gradient.
Now, we have τ is directly proportion to dθ/ dt
Observing dθ is not easy in case of fluid so it can also be written as
τ is directly proportional to du/ dy
τ =μdu/dy and this is known as the newton’s law of viscosity.
Where μ is the dynamic viscosity of the fluid
- SI unit of dynamic viscosity is N.s/ m² or pa. sec
- CGS unit of dynamic viscosity is dyne. s/ cm² or poise
- Relationship between pa. s and poise, 1 pa. s = 10poise
- Now we can define fluid as it is a substance which deforms continuously under action of a very small shear force or shear stress.
7. Kinematic Viscosity
Kinematic viscosity is defined as that ability of fluid by virtue of which fluid diffuses the disturbance occurring in molecular momentum. Mathematically it is represented as
ν = μ/ρ
Where ν is kinematic viscosity of fluid
μ is dynamic viscosity of fluid
ρ is density of fluid
- SI unit of kinematic viscosity is m²/s
- CGS unit is cm²/s or stokes
Effect of temperature on dynamic viscosity
a) Liquids (Fluid Types and Properties)
In liquid the viscosity is majorly due to cohesion, as we increase the temperature kinetic energy of the particles increases and they tend to move away from each other by which attraction force between the particle reduces thus cohesive force between particle reduces hence resulting in reduction of dynamic viscosity. Therefore dynamic viscosity of liquid decreases with increase in temperature.
μ= μ˳/1+ αT+ βT²
μ˳ = dynamic viscosity of liquid at 0ºC
α, β are constant and α>β
b) Gases (Fluid Types and Properties)
In gases viscosity is due to intermolecular momentum transfer. As we increase the temperature, momentum of molecule increases and when they collide with each other they exert more pressure to each other so the frictional force due to the collision of molecule increases because molecular momentum is increased. Dynamic viscosity of gases increases with respect to temperature.
μ = μ˳+ αT + βT²
μ˳ = dynamic viscosity of liquid at 0ºC
α, β are constant and α>β
So from above equation we have μ is directly proportional to T
8. Compressibility (β)
• It is defined as the ability to get compressed or ease of compression.
• It can also be defined as volumetric strain per compressive stress.
β = (-dV/V)/dP
Minus sign indicate reduction in volume
• Mass(m) = mass density (ρ) X volume (V)
m = ρV
• From the law of conservation of mass, we know that the mass is constant
Therefore, m= constant
ρV = constant
ρdV + Vdρ = 0
ρdV = -Vdρ
-dV/V = dρ/ρ this is the value of volumetric strain in terms of density.
Now we have compressibility,
Ββ = (dρ/ρ)/dP = dρ/ρ.dP
• From above we conclude that β is the function of density which means if density of a material is changing by exerting the pressure then the material is compressible and if the density is not changing by exerting the pressure then the material in incompressible.
9. Bulk Modulus (K)
- Bulk modulus is defined as the ratio of compressive stress to volumetric strain.
- Therefore we have bulk modulus inversely proportional compressibility.
- K= 1/β = ρdP/dρ
10. Vapor pressure
Vapour pressure is defined as the pressure exerted by the vapour of a liquidon the surface of the liquid.
- If vapor pressure is less than pressure acting on the surface of liquid then we have evaporation.
- If vapor pressure is equal to pressure acting on the surface of liquid then we have Boiling.
- There is a slight difference between vaporization, boiling and evaporation.
- Evaporation can occur at any temperature but it is a surface phenomenon. While vaporization is a phase conversion process.
Types of Fluid
1. Ideal Fluid
Ideal fluid is fluid which is in viscid, incompressible, no shear stress and constant normal stress. According to Newton’s law of viscosity,
τ = μdu/dy
Where μ is zero because fluid is in viscid
Hence, τ is also zero. So there will be no shear stress.
X axis represents rate of shear strain while y axis represents shear stress. For ideal fluid rate of shear strain increasing but the shear stress is zero throughout because the fluid is continuously deforming without offering any resistance.
2. Newtonian Fluid
Fluid which obeys Newton’s law of viscosity is known as Newtonian fluid.
τ = μdu/dy
Therefore, for Newtonian fluid τ is directly proportional to du/dy.
Slope of Newtonian fluid on graph of τ and du/dy is μ.
3. Non Newtonian Fluid
A fluid which does not follow the newton’s law of viscosity are categorised under this.
τ = m (du/dy) ͪ
Where m is consistency index and h is flow index
1) On the basis of value of h, non Newtonian fluids are of two types
If h is greater than 1 then the non Newtonian fluid is known as Dilatant fluid. They are shear thicking fluid means they get thicken up when we apply shear force on it. Example: starch suspension.
2) If h is less than 1 then the non Newtonian fluid is known as pseudo plastic fluid. They are shear thinning fluid mean its viscosity reduces when we apply shear force in it. Example: blood.
4. Bingham Plastic Fluid and Herschel Buckley Fluid
Fluid in which some initial value of stress is required to initiate the flow is known as Bingham plastic fluid or Herschel Buckley fluid.
Ττ = τy + m (du/dy) ͪ
Where m is consistency index, h is flow index and τy is yield shear stress τy value of shear stress is required to generate to initiate the flow and if it is not generated then the fluid will not flow and behaves like a solid.
When flow is initiated and fluid flow gives linear behavior after the application of yield shear stress these fluids are known as Bingham plastic fluid. When flow is initiated and fluid flow does not give linear behavior after the application of yield shear stress these fluids are known as Herschel Buckley fluid.
5. Thixotropic and Rheopectic Fluid
Viscosity of these fluids is time dependent. Their viscosity increases or decreases with respect to time. Thixotropic fluids are those fluids in which apparent viscosity with time decreases.
Example: Mixture of water and bentonite clay.
Rheopectic fluids are those fluids in which apparent viscosity with time increases. Example: Printer Ink (as the time increases it dries and its viscosity increases)